更佳的阅读体验

题目大意

有 \(n\) 台电脑排成一排。每次可以手动开启一台。若某台电脑未开启且它两侧的电脑均开启，则它会自动开启。求开启所有电脑的方案数。两种方案不同当且仅当对应的手动开启电脑的序列不同。
数据范围： \(3 \leqslant n \leqslant 400\) 。

解 - 参考这篇题解

如图：

那么我们需要处理的情况有两种：BBB片段和BGB片段

Part 1: BBB序列

所以手动开启长度为 \(n\) 的电脑的方案数为
\[ C^1_{n-1} + C^2_{n-1} + ... + C^{n-1}_{n-1} = 2^{n-1} \]

Part 2: BGB序列

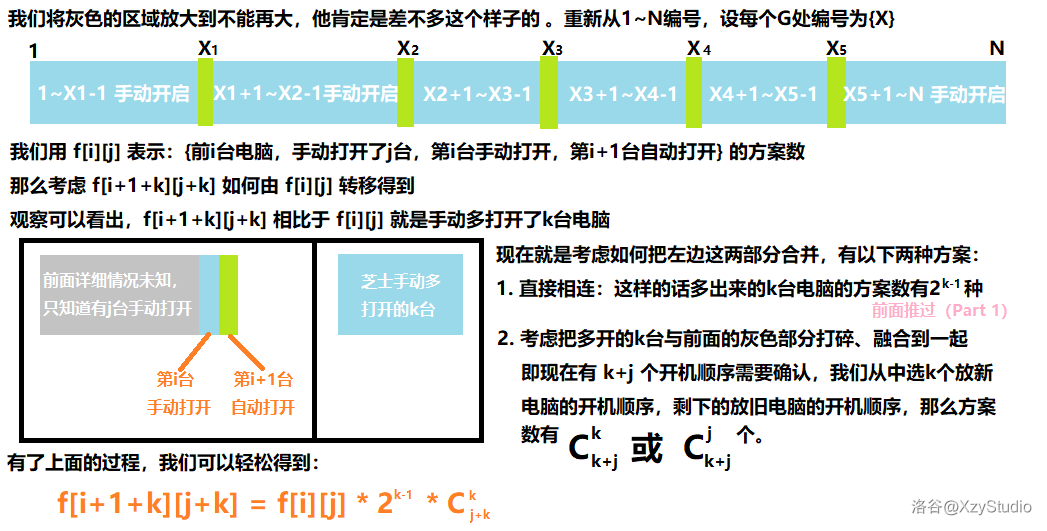
答案即：\[ \sum^n_{i=0} f[n][i] \]
\(i, j, k\)均通过枚举得到

用Windows画图花了好久，给个赞吧qwq

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 4e2 + 10;
long long C[N][N] , bit[N];
long long n , m , ans , f[N][N]; 
void init(int mod)
{
    bit[0] = 1;
    for(int i = 1 ; i <= N - 10 ; i ++) bit[i] = bit[i - 1] * 2 % mod; 
    for(int i = 0 ; i <= N - 10 ; i ++)
    {
        C[i][0] = 1;
        for(int j = 1 ; j <= i ; j ++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
    }
}
signed main()
{
    cin >> n >> m;
    init(m);
    for(int i = 1 ; i <= n ; i ++)
    {
        f[i][i] = bit[i - 1];
        for(int j = 0 ; j <= i ; j ++)
        {
            for(int k = 1 ; k + i + 1 <= n; k ++)
            {
                f[i + 1 + k][j + k] += f[i][j] * bit[k - 1] % m * C[j + k][k] % m;
                f[i + 1 + k][j + k] %= m; 
            }
        }
    }
    for(int i = 0 ; i <= n ; i ++) ans += f[n][i] , ans %= m;
    cout << ans << '\n';
    return 0;
}