换根 DP

树形 DP 中的换根 DP 问题又被称为二次扫描，通常不会指定根结点，并且根结点的变化会对一些值，例如子结点深度和、点权和等产生影响。

通常需要两次 DFS，第一次 DFS 预处理诸如深度，点权和之类的信息，在第二次 DFS 开始运行换根动态规划。

不妨令 \(u\) 为当前结点，\(v\) 为当前结点的子结点。首先需要用 \(s_i\) 来表示以 \(i\) 为根的子树中的结点个数，并且有 \(s_u=1+\sum s_v\)。显然需要一次 DFS 来计算所有的 \(s_i\)，这次的 DFS 就是预处理，我们得到了以某个结点为根时其子树中的结点总数。

考虑状态转移，这里就是体现＂换根＂的地方了。令 \(f_u\) 为以 \(u\) 为根时，所有结点的深度之和。

\(f_v\leftarrow f_u\) 可以体现换根，即以 \(u\) 为根转移到以 \(v\) 为根。显然在换根的转移过程中，以 \(v\) 为根或以 \(u\) 为根会导致其子树中的结点的深度产生改变。具体表现为：

• 所有在 \(v\) 的子树上的结点深度都减少了一，那么总深度和就减少了 \(s_v\)；

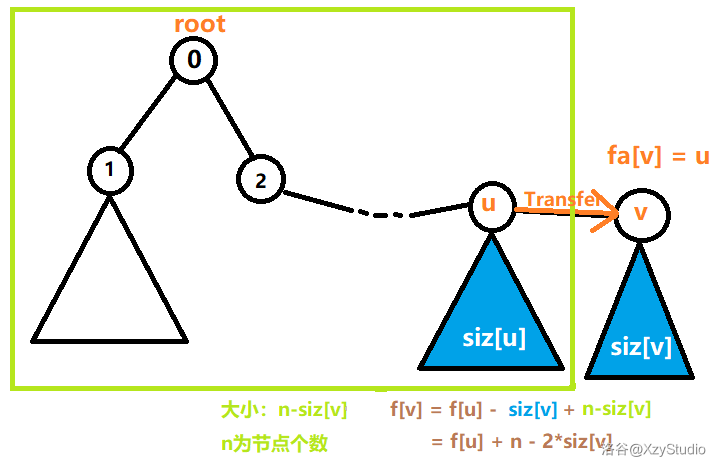
• 所有不在 \(v\) 的子树上的结点深度都增加了一，那么总深度和就增加了 \(n-s_v\) （为什么是 \(n-s_v\) 而不是 \(s_u\) ？见下图）；

根据这两个条件就可以推出状态转移方程 \(f_v = f_u - s_v + n - s_v=f_u + n - 2 \times s_v\)。

于是在第二次 DFS 遍历整棵树并状态转移 \(f_v=f_u + n - 2 \times s_v\)，那么就能求出以每个结点为根时的深度和了。最后只需要遍历一次所有根结点深度和就可以求出答案。

一图理解状态转移方程

参考代码：

#include <bits/stdc++.h>
using namespace std;

int head[1000010 << 1], tot;
long long n, sz[1000010], dep[1000010];
long long f[1000010];

struct node {
  int to, next;
} e[1000010 << 1];

void add(int u, int v) {  // 建图
  e[++tot] = {v, head[u]};
  head[u] = tot;
}

void dfs(int u, int fa) {  // 预处理dfs
  sz[u] = 1;
  dep[u] = dep[fa] + 1;
  for (int i = head[u]; i; i = e[i].next) {
    int v = e[i].to;
    if (v != fa) {
      dfs(v, u);
      sz[u] += sz[v];
    }
  }
}

void get_ans(int u, int fa) {  // 第二次dfs换根dp
  for (int i = head[u]; i; i = e[i].next) {
    int v = e[i].to;
    if (v != fa) {
      f[v] = f[u] - sz[v] * 2 + n;
      get_ans(v, u);
    }
  }
}

int main() {
  scanf("%lld", &n);
  int u, v;
  for (int i = 1; i <= n - 1; i++) {
    scanf("%d%d", &u, &v);
    add(u, v);
    add(v, u);
  }
  dfs(1, 1);
  for (int i = 1; i <= n; i++) f[1] += dep[i];
  get_ans(1, 1);
  long long int ans = -1;
  int id;
  for (int i = 1; i <= n; i++) {  // 统计答案
    if (f[i] > ans) {
      ans = f[i];
      id = i;
    }
  }
  printf("%d\n", id);
  return 0;
}