【模板】单源最短路径（弱化版）

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。
两个点之间可能有多条边，敬请注意。

输入格式

第一行包含三个整数 \(n,m,s\)，分别表示点的个数、有向边的个数、出发点的编号。
接下来 \(m\) 行每行包含三个整数 \(u,v,w\)，表示一条 \(u \to v\) 的，长度为 \(w\) 的边。

输出格式

输出一行 \(n\) 个整数，第 \(i\) 个表示 \(s\) 到第 \(i\) 个点的最短路径，若不能到达则输出 \(2^{31}-1\)。

样例 #1

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

样例说明 #1

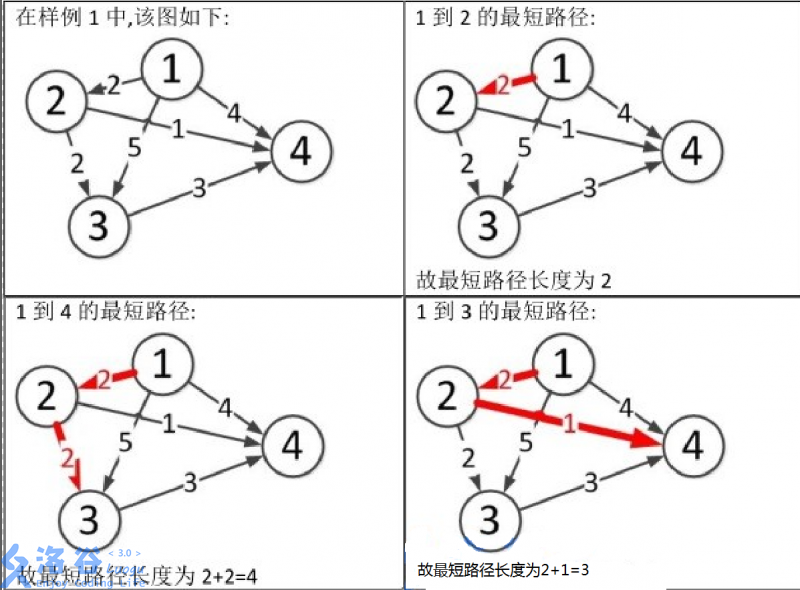
图片1到3和1到4的文字位置调换

提示

【数据范围】

对于 \(20\%\) 的数据：\(1\le n \le 5\)，\(1\le m \le 15\)；
对于 \(40\%\) 的数据：\(1\le n \le 100\)，\(1\le m \le 10^4\)；
对于 \(70\%\) 的数据：\(1\le n \le 1000\)，\(1\le m \le 10^5\)；
对于 \(100\%\) 的数据：\(1 \le n \le 10^4\)，\(1\le m \le 5\times 10^5\)，\(1\le u,v\le n\)，\(w\ge 0\)，\(\sum w< 2^{31}\)，保证数据随机。

来源

Luogu P3371，数据为本OJ生成的数据。