小 \(L\) 有一棵 \(n\) 个节点的树，其中有一些节点是关键节点。

小 \(M\) 会在树上选择一些**互不相交的**联通块，需要保证每个关键节点都至少被一个联通块包含。

若这些联通块的大小分别为 \(c_1,c_2 \dots c_k\) ，定义这些联通块的权值为 \(\sum \limits_{i=1}^k (c_i+T)\) 。

你需要对 \(l\le T \le r\) ，求出权值的最小值。可以参考样例解释进行理解。

输入格式

第一行包含三个数 \(n,l,r\) 。

第二行包含 \(n\) 个数 \(t_i\) ，若 \(t_i=1\) ，则点 \(i\) 为关键节点，否则 \(i\) 不为关键节点。

以下 \(n-1\) 行，每行 \(2\) 个数 \(u,v\)，表示一条边。

输出格式

\(r-l+1\) 个数，第 \(i\) 个数表示当 \(T=i+l-1\) 时的答案。

样例输入 1

7 1 4
0001010
7 4
5 6
7 2
5 1
6 3
2 5

样例输出 1

4
6
8
9

样例解释

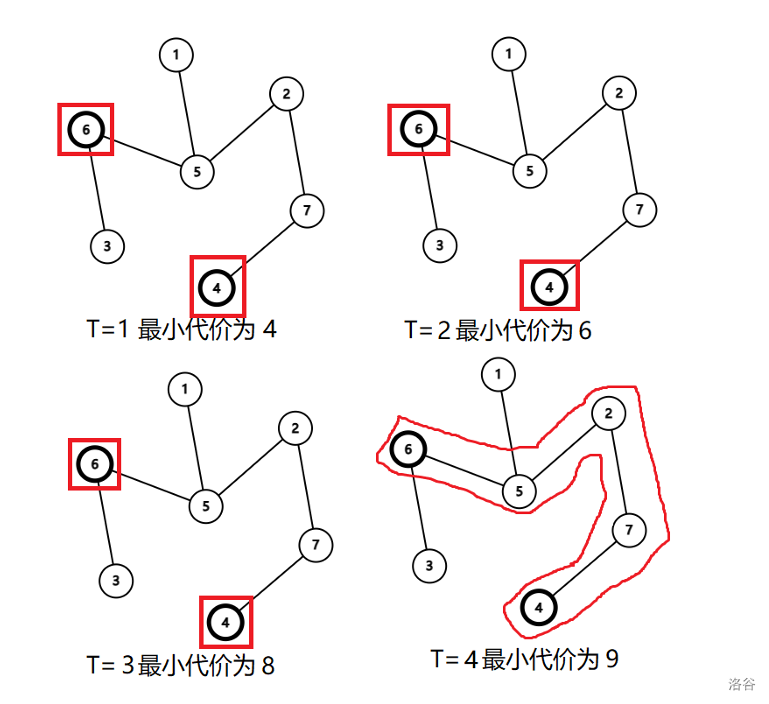
样例输入 2

见下发文件中的 ex_price2.in 。该样例满足数据点 1,2,3 的限制。

样例输出 2

见下发文件中的 ex_price2.out 。该样例满足满足数据点 1,2,3 的限制。

样例输入 3

见下发文件中的 ex_price3.in 。该样例满足数据点 4,5,6 的限制。

样例输出 3

见下发文件中的 ex_price3.out 。该样例满足数据点 4,5,6 的限制。

样例输入 4

见下发文件中的 ex_price4.in 。该样例满足数据点 9 的限制。

样例输出 4

见下发文件中的 ex_price4.out 。该样例满足数据点 9 的限制。

样例输入 5

见下发文件中的 ex_price5.in 。该样例满足数据点 10,11 的限制。

样例输出 5

见下发文件中的 ex_price5.out 。该样例满足数据点 10,11 的限制。

样例输入 6

见下发文件中的 ex_price6.in 。该样例满足数据点 16,17,18,19 的限制。

样例输出 6

见下发文件中的 ex_price6.out 。该样例满足数据点 16,17,18,19 的限制。

样例输入 7

见下发文件中的 ex_price7.in 。该样例满足数据点 20,21,22,23,24,25 的限制。

样例输出 7

见下发文件中的 ex_price7.out 。该样例满足数据点 20,21,22,23,24,25 的限制。

数据范围

数据点编号	限制
1,2,3	\(n \le 20\)
4,5,6	\(n \le 500\)
7,8,9	\(n \le 3 \times 10^3\)
10,11	\(n \le 10^4\)
12,13	\(R \le 10^3\)
14,15	\(L \ge 10^5\)
16,17,18,19	\(n \le 10^5\)
20,21,22,23,24,25	无

对于所有数据，保证 \(n \le 2 \times 10^5,1 \le l \le r\le n\) 。

另外，数据点 3,6,9,19,25 满足 \( \forall 1 \le i <n,\) 点 \(i\) 与点 \(i+1\) 连边。

下发文件

a_little_cut Round 2 下发文件