出题人太菜，暂无测试数据。

题目描述

灰灰现在有一个长条状的电路板，上面依次排列着接口\(1~N\)，灰灰为了实现某些功能，用电线将\(u, v\)两个接口连起来，这样的连接有\(M\)个，\(u\)与\(v\)之间不会同时连接多条线，且\(u \neq v\)
灰灰现在觉得他的电路板上的线有点乱，但是为了保证功能正常，他要求减去最少的线，使得剩余的线路没有交叉，并且剩余线路的总长度在所有方案中 最长

交叉状态定义如下：对于\(u_1, v_1, u_2, v_2\)，有两条无向边分别连接\(u_1, v_1\)和\(u_2, v_2\)，当且仅当\(u_1 < u_2\)且\(v_1 < v_2\)时，两条边交叉。
一条线路长度定义如下：对于一条连接\(u, v\)的线路，长度\(l = |u-v|\)

输入输出格式

输入格式

第一行两个整数\(N, M\)
接下来\(M\)行，每行两个整数\(u, v\)，表示有一条连接\(u, v\)的线路

输出格式

输出最优方案中剩余边长之和

样例

输入

10 8
1 3
2 1
3 6
4 5
5 7
6 10
9 4
10 8

输出

13

样例解释

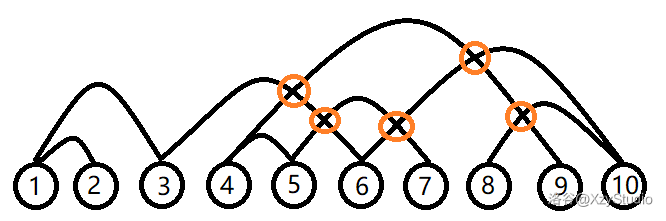
如图，共5个交叉，去除\(5 \rightarrow 7\)和\(4 \rightarrow 9\)最优，剩\(13\)

数据范围

测试点编号	特殊性质	数据规模
1~2	无	\(N, M \leqslant 10\)
3~4	无	\(N \leqslant 10, M \leqslant 100\)
5~8	无	\(N, M \leqslant 1000\)
9	\(v = u+2\)，\(u\)依次递增\(1\)	\(N, M \leqslant 1000\)
10	每个点至多连接一条边	\(N, M \leqslant 1000\)