该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

小 \(T\) 生活在 \(\omega\) 国。\(\omega \) 国有 \(n\) 个城市，由于 \(\omega\) 国已经高度发达，每两个城市间都有一座双向的时空隧道。连接 \(i,j\) 的时空隧道的通行时间为 \(t_{i,j}\) 。

生活在 \(\Omega\) 国的小 \(S\) ，想在假期去看望小 \(T\) 。但由于一些经济原因，小 \(S\) 只能申请到 \(n-1\) 条时空隧道的使用权。小 \(S\) 想让这 \(n-1\) 条时空隧道连通整个 \(\omega\) 国。

同时，小 \(S\) 会在 \(u\) 点进入 \(\omega\) 国。由于时空隧道的特殊性，从 \(i\) 到 \(j\) 的通行时间 \(w_{i,j}\) 为：设 \(i\) 到 \(j\) 不经过同一座城市两次的路径为 \(i,p_1,\dots p_k,j\) ，则 \(w_{i,j}=\min(t_{i,p_1},\min_\limits{i=1}^{k-1} t_{p_i,p_{i+1}},t_{p_k,j})\) 。简要的说，就是 \(i\) 到 \(j\) 在生成树上的唯一简单路径上边权的最小值。

注意此时只有有使用权的 \(n-1\) 条时空隧道可以使用，因此，路径是唯一的 。

对于一种使用权的方案，定义其代价为 \(\sum _\limits{i=1}^{n} w_{u,i}\) 。小 \(S\) 想让你对于所有起点 \(u\) ，求出此时所有方案中代价的最小值。

输入格式

第一行包含一个整数 \(n\) 。

以下 \(n-1\) 行中，第 \(i\) 行包含 \(n-i\) 个数 。

第 \(i\) 行的第 \(j\) 个数表示 \(t_{i,{i+j}}\) 。

输出格式

\(n\) 个数，第 \(i\) 行的数表示起点 \(i\) 的答案。

样例输入1

3
1 2
3

样例输出1

2
2
3

样例解释

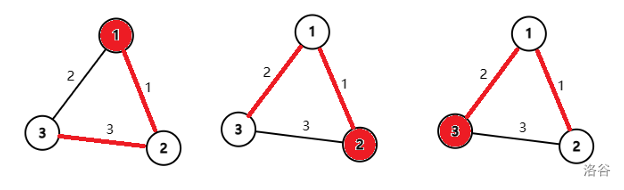
红点表示起点，红色的边表示有使用权的边。\(i=1,2,3\) 的最小代价分别为 \(2,2,3\) 。

样例输入 2

见下发文件中的 ex_travel2.in 。该样例满足数据点 1 的限制。

样例输出 2

见下发文件中的 ex_travel2.out 。该样例满足数据点 1 的限制。

样例输入 3

见下发文件中的 ex_travel3.in 。该样例满足数据点 6 的限制。

样例输出 3

见下发文件中的 ex_travel3.out 。该样例满足数据点 6 的限制。

样例输入 4

见下发文件中的 ex_travel4.in 。该样例满足数据点 9 的限制。

样例输出 4

见下发文件中的 ex_travel4.out 。该样例满足数据点 9 的限制。

样例输入 5

见下发文件中的 ex_travel5.in 。该样例满足数据点 16,17,18,19 的限制。

样例输出 5

见下发文件中的 ex_travel5.out 。该样例满足数据点 16,17,18,19 的限制。

数据范围与提示

测试点编号	限制
1,2	\(n \le 6\)
3,4	\(n \le 9\)
5,6	\(n \le 15\)
7,8,9	\(n \le 100\)
10	\(t_{i,j}=1\)
11,12	若 \(j=i+1\) 则 \(t_{i,j}=1\) ，否则 \(t_{i,j}=10^9\)
13,14,15	\(n \le 10^3\)
16,17,18,19,20	\(n \le 2 \times 10^3\)

对于所有数据，保证 \(n \le 2 \times 10^3,1 \le t_{i,j} \le 10^9\) 。

另外，数据点 2,4,6,9,15,20 保证 \(t_{i,j} \le n\) 。

本题输入规模较大，建议选手使用关流 cin 或快速读入。

下发文件

a_little_cut Round 2 下发文件